Dados e relações em árvores
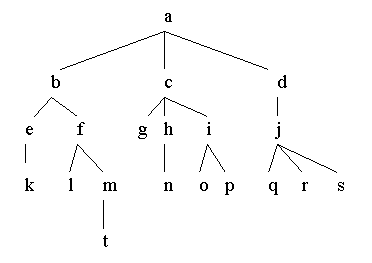
Considere o seguinte diagrama de árvore.
O arquivo '2_6.pl' tem uma representação para esta árvore e definições de predicado para fazer algum processamento da árvore. Observe o uso de operadores Prolog em algumas das definições
/* The tree database */
:- op(500,xfx,'is_parent').
a is_parent b. c is_parent g. f is_parent l. j is_parent q.
a is_parent c. c is_parent h. f is_parent m. j is_parent r.
a is_parent d. c is_parent i. h is_parent n. j is_parent s.
b is_parent e. d is_parent j. i is_parent o. m is_parent t.
b is_parent f. e is_parent k. i is_parent p.
/* X and Y are siblings */
:- op(500,xfx,'is_sibling_of').
X is_sibling_of Y :- Z is_parent X,
Z is_parent Y,
X \== Y.
/* X and Y are on the same level in the tree. */
:-op(500,xfx,'is_same_level_as').
X is_same_level_as X .
X is_same_level_as Y :- W is_parent X,
Z is_parent Y,
W is_same_level_as Z.
/* Depth of node in the tree. */
:- op(500,xfx,'has_depth').
a has_depth 0 :- !.
Node has_depth D :- Mother is_parent Node,
Mother has_depth D1,
D is D1 + 1.
/* Locate node by finding a path from root down to the node. */
locate(Node) :- path(Node),
write(Node),
nl.
path(a). /* Can start at a. */
path(Node) :- Mother is_parent Node, /* Choose parent, */
path(Mother), /* find path and then */
write(Mother),
write(' --> ').
/* Calculate the height of a node, length of longest path to
a leaf under the node. */
height(N,H) :- setof(Z,ht(N,Z),Set), /* See section 2.8 for 'setof'. */
max(Set,0,H).
ht(Node,0) :- leaf(Node), !.
ht(Node,H) :- Node is_parent Child,
ht(Child,H1),
H is H1 +1.
leaf(Node) :- not(is_parent(Node,Child)). /* Node grounded */
max([],M,M).
max([X|R],M,A) :- (X > M -> max(R,X,A) ; max(R,M,A)).O relacionamento 'is_sibling_of' testa se dois nós têm um pai comum na árvore. Por exemplo,
?- h is_sibling_of S.
S=g ;
S=i ;
noObserve o uso do literal X \== Y, que é bem-sucedido apenas no caso de X e Y não serem combinados (ligados ao mesmo valor).
O relacionamento 'is_same_level_as' testa se dois nós estão no mesmo nível na árvore.
O predicado 'depth' calcula a profundidade de um nó na árvore (quantas arestas da raiz). Por exemplo,
?- t has_depth D.
D=4Segue uma definição alternativa de 'depth' usando a implicação do Prolog:
N has_depth D :- N == 'a' -> D=0 ;
Mother is_parent N,
Mother has_depth D1,
D is D1 + 1.O predicado 'locate' calcula e imprime um caminho da raiz para um nó. Por exemplo,
?- locate(n).
a --> c --> h --> nO predicado 'leaf' define uma folha como um nó que não é um pai. Observe a variável livre dentro da negação. Isso está correto, pois se o nó tiver algum filho, o nó não é uma folha.
O predicado 'height' calcula a altura de um nó -- definido como o comprimento do caminho mais longo para uma folha sob o nó. Esta definição usa listas e o predicado Prolog de segunda ordem 'setof'. Continuaremos a discussão de 'height' e 'setof' na seção 2.8.
Carregue o programa no ambiente Prolog e teste o programa emitindo vários objetivos.
Exercício 2.6.1 Escreva uma definição Prolog para 'ancestor(X, Y)' com o significado pretendido de que "X é um ancestral de Y na árvore". Preste atenção: a recursão deve ser até o topo da árvore ou até a base da árvore?
Exercício 2.6.2 Conforme escrito, 'leaf/1' é um teste quando o Node está definido. Reformule 'leaf/1' para que o objetivo ?- leaf(X) retorne X valores que são folhas da árvore.
Exercício 2.6.3 Formule definições para uma árvore genealógica humana usando as relações 'masculino', 'feminino', 'pai', 'pai', 'mãe', 'irmão', 'avô', 'avó', 'avô', ' primo ',' tia 'e' tio '. Deixe que 'masculino', 'feminino', 'pai' sejam as relações fundamentais e defina as outras em termos destas (através de regras).
Veja Também
- Código do Prolog para esta seção.
- 2.7 Listas em Prolog
- 2.8 Troco para um dólar
- Prolog Tutorial Sumário