Busca-αβ no Prolog
Esta seção adapta a estrutura de Busca α&beta em The Art of Prolog, de L. Sterling e E. Shapiro (1986)[1] para jogar o jogo da velha (O e X). Um dos objetivos é estudar essa estrutura testando a adaptação ao jogo da velha. Outro propósito pretendido é ter um agente especialista Prolog em 'jogo da velha' que possa jogar contra a interface GUI desenvolvida na Seção 8.4.
Representando o Tabuleiro do Jogo da Velha no Prolog
Para representar o tabuleiro de jogo da velha, usamos uma lista Prolog. O tabuleiro vazio, antes do jogo começar é
_|_|_
_|_|_ ~ [_Z1,_Z2,_Z3,_Z4,_Z5,_Z6,_Z7,_Z8,_Z9]
_|_|_ | 1st row | 2nd row | third row |Depois cada jogador de jogar dois movimentos, o tabuleiro fica assim...
o|_|_
o|x|x ~ [o,_Z2,_Z3,o,x,x,_Z7,_Z8,_Z9]
_|_|_A razão para esta representação um tanto obscura é evitar ter que processar uma representação de lista para o tabuleiro. Em vez disso, um jogador marca o tabuleiro vinculando uma variável livre.
:- dynamic board/1.
:- retractall(board(_)).
:- assert(board([_Z1,_Z2,_Z3,_Z4,_Z5,_Z6,_Z7,_Z8,_Z9])).
%%%%%
%% Generate possible marks on a free spot on the board.
%% Use mark(+,+,-X,-Y) to query/generate possible moves (X,Y).
%%%%%
mark(Player, [X|_],1,1) :- var(X), X=Player.
mark(Player, [_,X|_],2,1) :- var(X), X=Player.
mark(Player, [_,_,X|_],3,1) :- var(X), X=Player.
mark(Player, [_,_,_,X|_],1,2) :- var(X), X=Player.
mark(Player, [_,_,_,_,X|_],2,2) :- var(X), X=Player.
mark(Player, [_,_,_,_,_,X|_],3,2) :- var(X), X=Player.
mark(Player, [_,_,_,_,_,_,X|_],1,3) :- var(X), X=Player.
mark(Player, [_,_,_,_,_,_,_,X|_],2,3) :- var(X), X=Player.
mark(Player, [_,_,_,_,_,_,_,_,X|_],3,3) :- var(X), X=Player.
%%%%%
%% Record a move: record(+,+,+).
%%%%%
record(Player,X,Y) :-
retract(board(B)),
mark(Player,B,X,Y),
assert(board(B)).Por exemplo, depois que este código é carregado, considere o seguinte objetivo ...
?- board(B),mark(o,B,X,Y).
B = [o, _G286, _G289, _G292, _G295, _G298, _G301, _G304, _G307] X = 1 Y = 1 ;
B = [_G283, o, _G289, _G292, _G295, _G298, _G301, _G304, _G307] X = 2 Y = 1 ;
B = [_G283, _G286, o, _G292, _G295, _G298, _G301, _G304, _G307] X = 3 Y = 1 ;
B = [_G283, _G286, _G289, o, _G295, _G298, _G301, _G304, _G307] X = 1 Y = 2 ;
B = [_G283, _G286, _G289, _G292, o, _G298, _G301, _G304, _G307] X = 2 Y = 2 ;
B = [_G283, _G286, _G289, _G292, _G295, o, _G301, _G304, _G307] X = 3 Y = 2 ;
B = [_G283, _G286, _G289, _G292, _G295, _G298, o, _G304, _G307] X = 1 Y = 3 ;
B = [_G283, _G286, _G289, _G292, _G295, _G298, _G301, o, _G307] X = 2 Y = 3 ;
B = [_G283, _G286, _G289, _G292, _G295, _G298, _G301, _G304, o] X = 3 Y = 3 ;
NoIsso ilustra que todos os movimentos podem ser gerados pelo backtracking nas cláusulas de marca. Agora, vamos primeiro registrar um 'xin' no centro e, em seguida, gerar todos os movimentos subsequentes possíveis para 'o' ...
?- record(x,1,1), board(B), findall((X,Y),mark(o,B,X,Y),Moves).
B = [x, _G370, _G373, _G376, _G379, _G382, _G385, _G388, _G391]
X = _G186
Y = _G187
Moves = [ (2, 1), (3, 1), (1, 2), (2, 2), (3, 2), (1, 3), (2, 3), (3, 3)]
Yes
?- board(B).
B = [x, _G234, _G237, _G240, _G243, _G246, _G249, _G252, _G255]
YesObserve cuidadosamente que o registro de fato afirma um movimento, mas essa marca simplesmente encontra todos os movimentos possíveis (sem realmente registrá-los). Precisamos de uma função de avaliação que meça o quão bom é um tabuleiro para um jogador. Usamos o conhecido que mede a diferença entre as linhas de jogo abertas para cada jogador,
value(Board) = (# open lines for o - # open lines for x)Valores maiores favorecem 'o', valores menores favorecem 'x'. Nosso campeão é o (computador) cujos algoritmos abaixo buscarão maximizar o valor de um movimento. Os algoritmos assumem que 'x' procuraria minimizar o valor. Um tabuleiro vencedor para 'o' tem valor 100, um tabuleiro vencedor para 'x' tem valor -100.
%%%%%
%% Calculate the value of a position, o maximizes, x minimizes.
%%%%%
value(Board,100) :- win(Board,o), !.
value(Board,-100) :- win(Board,x), !.
value(Board,E) :-
findall(o,open(Board,o),MAX),
length(MAX,Emax), % # lines open to o
findall(x,open(Board,x),MIN),
length(MIN,Emin), % # lines open to x
E is Emax - Emin.
%%%%%
%% A winning line is ALREADY bound to Player.
%% win(+Board,+Player) is true or fail.
%% e.g., win([P,P,P|_],P). is NOT correct, because could bind
%%%%%
win([Z1,Z2,Z3|_],P) :- Z1==P, Z2==P, Z3==P.
win([_,_,_,Z1,Z2,Z3|_],P) :- Z1==P, Z2==P, Z3==P.
win([_,_,_,_,_,_,Z1,Z2,Z3],P) :- Z1==P, Z2==P, Z3==P.
win([Z1,_,_,Z2,_,_,Z3,_,_],P) :- Z1==P, Z2==P, Z3==P.
win([_,Z1,_,_,Z2,_,_,Z3,_],P) :- Z1==P, Z2==P, Z3==P.
win([_,_,Z1,_,_,Z2,_,_,Z3],P) :- Z1==P, Z2==P, Z3==P.
win([Z1,_,_,_,Z2,_,_,_,Z3],P) :- Z1==P, Z2==P, Z3==P.
win([_,_,Z1,_,Z2,_,Z3,_,_],P) :- Z1==P, Z2==P, Z3==P.
%%%%%
%% A line is open if each position is either free or equals the Player
%%%%%
open([Z1,Z2,Z3|_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,_,_,Z1,Z2,Z3|_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,_,_,_,_,_,Z1,Z2,Z3],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([Z1,_,_,Z2,_,_,Z3,_,_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,Z1,_,_,Z2,_,_,Z3,_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,_,Z1,_,_,Z2,_,_,Z3],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([Z1,_,_,_,Z2,_,_,_,Z3],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,_,Z1,_,Z2,_,Z3,_,_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
%%%%%
%% Calculate the value of a position, o maximizes, x minimizes.
%%%%%
value(Board,100) :- win(Board,o), !.
value(Board,-100) :- win(Board,x), !.
value(Board,E) :-
findall(o,open(Board,o),MAX),
length(MAX,Emax), % # lines open to o
findall(x,open(Board,x),MIN),
length(MIN,Emin), % # lines open to x
E is Emax - Emin.Por exemplo,
?- value([_X,o,o,_Y,o,x,x,_Z,x],V).
V = 0O leitor deve experimentar vários exemplos de tabuleiro e também calcular o valor por inspeção.
Adaptando a Busca-αβ para o Jogo da Velha
O algoritmo de Busca-αβ calcula qual movimento será melhor para um jogador. O algoritmo maximiza o valor de 'o' e minimiza o valor de 'x'. Segue um exemplo de estrutura de código básica ...
alpha_beta(Player,0,Position,_Alpha,_Beta,_NoMove,Value) :-
value(Position,Value).
alpha_beta(Player,D,Position,Alpha,Beta,Move,Value) :-
D > 0,
findall((X,Y),mark(Player,Position,X,Y),Moves),
Alpha1 is -Beta, % max/min
Beta1 is -Alpha,
D1 is D-1,
evaluate_and_choose(Player,Moves,Position,D1,Alpha1,Beta1,nil,(Move,Value)).
evaluate_and_choose(Player,[Move|Moves],Position,D,Alpha,Beta,Record,BestMove) :-
move(Player,Move,Position,Position1),
other_player(Player,OtherPlayer),
alpha_beta(OtherPlayer,D,Position1,Alpha,Beta,_OtherMove,Value),
Value1 is -Value,
cutoff(Player,Move,Value1,D,Alpha,Beta,Moves,Position,Record,BestMove).
evaluate_and_choose(_Player,[],_Position,_D,Alpha,_Beta,Move,(Move,Alpha)).
cutoff(_Player,Move,Value,_D,_Alpha,Beta,_Moves,_Position,_Record,(Move,Value)) :-
Value >= Beta, !.
cutoff(Player,Move,Value,D,Alpha,Beta,Moves,Position,_Record,BestMove) :-
Alpha < Value, Value < Beta, !,
evaluate_and_choose(Player,Moves,Position,D,Value,Beta,Move,BestMove).
cutoff(Player,_Move,Value,D,Alpha,Beta,Moves,Position,Record,BestMove) :-
Value =< Alpha, !,
evaluate_and_choose(Player,Moves,Position,D,Alpha,Beta,Record,BestMove).
other_player(o,x).
other_player(x,o).Para testar o código da linha de comando do Prolog, adicionamos algumas instruções ...
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% For testing, use h(+,+) to record human move,
%%% supply coordinates. Then call c (computer plays).
%%% Use s to show board.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
h(X,Y) :- record(x,X,Y), showBoard.
c :-
board(B),
alpha_beta(o,2,B,-200,200,(X,Y),_Value), % <=== NOTE
record(o,X,Y), showBoard.
showBoard :-
board([Z1,Z2,Z3,Z4,Z5,Z6,Z7,Z8,Z9]),
write(' '),mark(Z1),write(' '),mark(Z2),write(' '),mark(Z3),nl,
write(' '),mark(Z4),write(' '),mark(Z5),write(' '),mark(Z6),nl,
write(' '),mark(Z7),write(' '),mark(Z8),write(' '),mark(Z9),nl.
s :- showBoard.
mark(X) :- var(X), write('#').
mark(X) :- \+var(X),write(X).Agora, considere as seguintes interações ...
?- s. % show the board
# # #
# # #
# # #
Yes
?- h(2,1). % Human marks x at 2,1 (not best)
# x #
# # #
# # #
Yes
?- c. % computer thinks, moves to 2,2
# x #
# o #
# # #
Yes
?- h(1,1). % Human moves to 1,1
x x #
# o #
# # #
Yes
?- c. % computer's move. SEE ANALYSIS BELOW
x x o
# o #
# # #
... etc.... é um empate.
O programa Prolog foi projetado para que o estado do jogo da velha seja armazenado após cada jogo, ao invés de um programa contínuo que interage alternadamente com os jogadores. A razão para esta escolha de design é que conectaremos o jogador Prolog de 'Jogo da Velha' com uma GUI Java na Seção 8.4. O programa Java também armazenará o estado do tabuleiro atual. Desta forma, Prolog e o Java terão apenas que se comunicar, dizendo ao outro jogador qual é o movimento: um par de números X,Y.
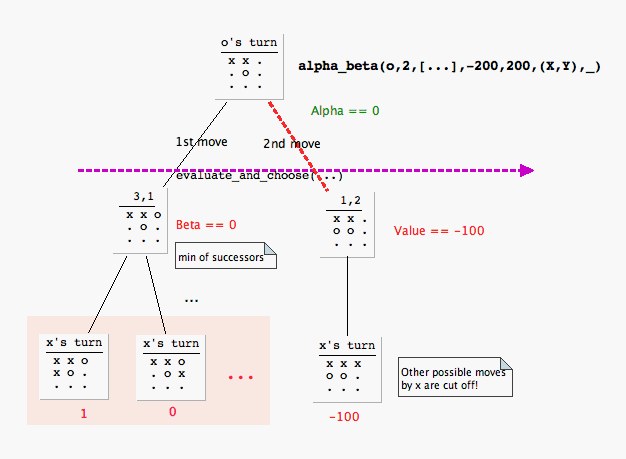
Vejamos o que acontece quando Prolog calcula o último movimento mostrado no jogo acima. O diagrama a seguir ilustra graficamente o que acontece com as escolhas de 'o' além do primeiro movimento possível (e criticamente melhor). Todos os movimentos são expandidos na ordem gerada pelo programa. O segundo movimento possível [x,x,_,o,o,_,_,_,_] dá a 'x' a oportunidade de escolher sua vitória [x,x,x,o,o,_,_,_,_]. Nosso maximizador, 'o', não tolerará isso e não continuará a buscar. O α-cutoff é a aresta vermelha tracejada da raiz para a escolha da segunda camada: Observe que 'cuttoff' é chamado por 'evaluate_and_choose' que pode, portanto, truncar as possibilidades! O valor de backup Alpha == 0 foi obtido da busca mais à esquerda: O melhor que pode ser garantido com este movimento.
O algoritmo αβ oferece muito mais poder do que o necessário para jogar o jogo da velha.
A vantagem real que a busca-αβ traz para um jogo mais complexo deriva de sua capacidade de cortar a árvore de busca para a busca que antecipa muitos outros movimentos. Sterling e Shapiro (1986)[1] fornecem um exemplo para o 'jogo de Kalah'. A complexidade do Kalah aproveita melhor a busca-αβ, assim como outros jogos mais complicados.
É possível que versões futuras deste Prolog Tutorial estudem jogos mais complexos.
A referência Principles of Artificial Intelligence de Nilsson (1980)[2] tem uma boa discussão sobre a busca-αβ e usa o jogo da velha como um exemplo motivador.
Veja Também
- Código do Prolog para o jogo da velha discutido nesta seção.
- 8.2 Um Jogo da Velha contra o oponente do Prolog (§5.3) com Java GUI
- Prolog Tutorial Sumário
Referências
- ↑ Ir para: 1,0 1,1 Sterling, Leon, and Shapiro, Ehud, The Art of Prolog, MIT Press, 1986.
- ↑ Nilsson, N., Principles of Artificial Intelligence, Tioga, 1980.