Ações e Planejamento

Nesta seção, apresentamos uma abordagem simplificada para gerar planos de ação para um robô hipotético. A situação básica envolve blocos em uma mesa. Os blocos individuais estão sobre a mesa ou podem ser empilhados em cima de outros blocos. Apenas um bloco caberá diretamente em cima de outro e os blocos não podem se sobrepor. Supõe-se que o robô seja capaz de mover apenas um bloco por vez, portanto, para mover um bloco específico que tem outros blocos empilhados em cima dele, o robô deve primeiro desempilhar os blocos até que o bloco específico tenha seu topo vazio.

Fig. 2.19.1

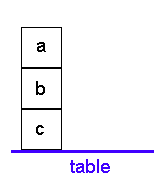
A situação retratada na imagem será representada pelas seguintes cláusulas:

  
on(a,b).    
on(b,c).    
on(c,table).

Poderíamos pensar na parte de nosso programa que dá a definição de 'on' como uma espécie de "memória" onde o estado atual do mundo dos blocos é registrado. O resto do programa envolverá regras sobre como realizar várias tarefas envolvendo o mundo dos blocos. Conforme as metas de rearranjo são satisfeitas, as alterações serão feitas na "memória" de estados do mundo usando 'assert' e 'retract'. Por exemplo, se o bloco 'a' for movido do topo de 'b' para a mesa, isso equivaleria a remover (retract) on(a,b) e afirmar (assert) on(a,table).

Fig. 2.19.2

  
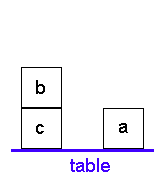
on(a,table).
on(b,c).    
on(c,table).

Vamos registrar esta ação declarando move(a,b,table) no programa. A parte do programa que define 'move' será o "quadro de ações" registrando um plano. Aqui está uma especificação de ação não recursiva sobre como colocar um bloco em outro:

  
put_on(A,B) :-
     A \== table,
     A \== B,
     on(A,X),
     clear(A),
     clear(B),
     retract(on(A,X)),
     assert(on(A,B)),
     assert(move(A,X,B)).

clear(table).
clear(B) :- 
     not(on(_X,B)).

Esta especificação de ação tem a forma

  
action :- preconditions,
          retract(affected_old_properties),
          assert(new_properties).

Em uma especificação de ação não recursiva, as pré-condições não conterão outras ações. Assim, no exemplo até agora,

?- put_on(a,table).
yes

?- listing(on), listing(move).

on(b,c).
on(c,table).
on(a,table).

move(a,b,table).

yes

?- put_on(c,a).
no

O último objetivo falha, pois um bloco deve ter um topo vazio para ser movido. portanto

  
?- put_on(b,table), put_on(c,a).
yes

é bem-sucedido porque 'b' é movido para fora de 'c' antes que 'c' seja movido para o topo de 'a'. Observe bem que as especificações de ação não alteram as propriedades que não são afetadas pela ação, porque as propriedades não afetadas não são recolhidas. A tarefa de capturar esse comportamento desejado é chamada de 'problema de quadro' (frame problem).

Aqui está uma especificação de ação recursiva para blocos móveis:

r_put_on(A,B) :-
     on(A,B).
r_put_on(A,B) :-
     not(on(A,B)),
     A \== table,
     A \== B,
     clear_off(A),        /* N.B. "action" used as precondition */
     clear_off(B),
     on(A,X),
     retract(on(A,X)),
     assert(on(A,B)),
     assert(move(A,X,B)).

clear_off(table).    /* Means there is room on table */
clear_off(A) :-      /* Means already clear */
     not(on(_X,A)).
clear_off(A) :-
     A \== table,
     on(X,A),
     clear_off(X),      /* N.B. recursion */
     retract(on(X,A)),
     assert(on(X,table)),
     assert(move(X,A,table)).

Uma especificação de ação recursiva pode ter a forma

action :-  preconditions or actions,
           retract(affected_old_properties),
           assert(new_properties).

Suponha novamente que a situação original se mantém (e que as cláusulas 'move' anteriores foram retiradas):

on(a,b).
on(b,c).
on(c,table).
Now,

   

?- r_put_on(c,a).
yes

?- listing(on), listing(move).

on(a,table).
on(b,table).
on(c,a).

move(a,b,table).
move(b,c,table).
move(c,table,a).

yes

A ação 'put_on' chamou recursivamente a ação 'clear_off' para que 'c' pudesse ser colocado em cima de 'a'.

Vamos agora adicionar ao programa algumas cláusulas para que uma lista de propriedades 'on' possa ser estabelecida em conjunto.

  
do(Glist) :- 
      valid(Glist), 
      do_all(Glist,Glist). 

valid(_).                          /* Temporary. See Exercise 2.19.1 */
   
do_all([G|R],Allgoals) :-          /* already true now */
     call(G),
     do_all(R,Allgoals),!.         /* continue with rest of goals */

do_all([G|_],Allgoals) :-          /* must do work to achieve */
     achieve(G),
     do_all(Allgoals,Allgoals).    /* go back and check previous goals */
do_all([],_Allgoals).              /* finished */

achieve(on(A,B)) :-
     r_put_on(A,B).

O programa agora pode ser usado fornecendo um objetivo principal da forma ?- do([...]), onde a lista contém várias instruções de subobjetivo on(-,-) (sem variáveis). Suponha que a situação inicial original seja mantida novamente; isso é,

on(a,b).
on(b,c),
on(c,table).

Consider the Prolog goal

  
?- do([on(a,table),on(b,a),on(c,b)]).
yes

?- listing(on), listing(move).
on(a,table).
on(b,a).
on(c,b).

move(a,b,table).
move(b,c,a).
move(c,table,b).

yes

O leitor deve tentar a meta e listar o programa resultante para verificar parcialmente se funciona da maneira que afirmamos. Este programa não faz nada de especial com o plano, a não ser incorporá-lo ao final do programa. Para gerar outro plano para a mesma configuração inicial, mas condições de objetivo diferentes, pode-se recarregar primeiro o planning.pro. Este inconveniente pode ser eliminado de várias maneiras, dependendo de como se pretende usar o programa (veja os exercícios para mais informações).

Preste atenção especial em como o programa tenta satisfazer uma lista de objetivos individuais. A definição do predicado 'do-all' no programa deve ser estudada cuidadosamente. Ao satisfazer uma lista de objetivos individuais, cada objetivo é trabalhado da esquerda para a direita. Se uma meta individual já estiver satisfeita, prossiga para o próximo objetivo. Caso contrário, satisfaça o objetivo atual, mas volte ao início da lista para verificar se os objetivos anteriores ainda foram satisfeitos. Trabalhe com eles novamente se eles ainda não estiverem satisfeitos. Faça isso repetidamente até que todos os objetivos individuais da lista sejam satisfeitos (se possível).

O sistema de planejamento STRIPS, descrito em Nilsson (1980), utilizou operadores que consistem em três componentes:

  
Fórmula de pré-condição, que deve ser verdadeira para que o
   operador a ser aplicável;

Delete-list, que consiste em predicados tornados falsos pela
   ação;

Add-list, que consiste em predicados tornados verdadeiros pela
   ação.

A última cláusula 'clear_off' pode ser caracterizada da maneira STRIPS, da seguinte forma:

  
clear_off(A) :
   Pré-condição: A \== table, on(X,A), clear_off(X)
  
   Delete-list: on(X,A)

   Add-list: on(X,table), move(X,A,table)

Na verdade, isso corresponderia à versão recursiva de STRIPS (RSTRIPS) pela mesma razão que nosso programa usou especificações de ação recursiva. O programa apresentado aqui usa Prolog como mecanismo de controle de inferência, enquanto o STRIPS tinha suas próprias estratégias de inferência e controle. Um bom projeto seria ler mais sobre STRIPS e implementá-lo novamente no Prolog.

O programa de planejamento Prolog ilustra várias outras questões de planejamento. Uma coisa importante a notar é que as metas individuais podem não ser independentes umas das outras. Por exemplo, usando a configuração inicial original, suponha que apresentamos o objetivo

?- do([on(c,b),on(b,a),on(a,table)]).

que é o reverso do objetivo anterior. Desta vez, o plano a seguir é gerado.

move(a,b,table).
move(b,c,table).
move(c,table,b).
move(c,b,table).
move(b,table,a).
move(c,table,b).

Compare este plano com o gerado anteriormente. Esse plano tem movimentos redundantes (como os dois do meio) e, de outra forma, não atinge a conjunção final de objetivos de maneira tão eficiente quanto o plano para o primeiro objetivo. Observe que a primeira tentativa foi mais eficiente porque procurou satisfazer primeiro as condições que representavam os blocos "inferiores" no plano final acabado e, em seguida, procurou satisfazer as condições que representavam os blocos "superiores" no plano acabado. Isso ilustra que os objetivos individuais em uma lista de objetivos conjuntos podem não ser independentes.

Na literatura de planejamento, essa condição é chamada de linearidade; linearidade significa que os sub-objetivos individuais podem ser satisfeitos sequencialmente em qualquer ordem arbitrária. Nosso exemplo mostra que a linearidade (ou independência) nem sempre é o caso. Além disso, alguns objetivos conjuntivos nem mesmo são possíveis. Por exemplo,

?- do([on(a,b),on(b,a)].

representa uma lista de objetivos incompatíveis: nem ambos os objetivos podem ser verdadeiros ao mesmo tempo, segundo as suposições feitas. O que acontecerá se alguém perguntar esse objetivo?

Exercício 2.19.1 Formule um conceito a respeito de uma lista válida de objetivos, isto é, se todos os objetivos podem ser verdadeiros em conjunto para blocos físicos reais, e projete um programa Prolog para testar se uma lista de objetivos é válida. Lembre-se de que a intenção original era não permitir que os blocos se sobreponham. Observe que [on(a,b),on(b,a)] é logicamente consistente, mas não é válido.

Exercício 2.19.2 Elimine a afirmação(assert) e a retração(retract) do programa usando parâmetros extras apropriados (representando listas de estado e listas de ação) nas definições. Os puristas do Prolog podem preferir esta nova versão porque ela não produz os efeitos colaterais do 'assert' e 'retract'.

Exercício 2.19.3 Escreva um programa que possa detectar e eliminar etapas redundantes em um plano.

O Exercício 2.19.1 é especialmente interessante. Observe que a validade deve capturar o significado de "fisicamente possível". O uso do termo válido difere, mas está diretamente relacionado ao termo de mesmo nome da lógica. Na lógica, "válido" significa verdadeiro em todas as interpretações possíveis. Aqui, "válido" significa verdadeiro em todas as interpretações pretendidas para o mundo dos blocos.

Gostaríamos de poder fazer as seguintes condições:

• Condição de Solidez: Se 'P0' é um programa inicial especificando um conjunto válido de condições ativas, e se 'a1, a2, ..., an' é uma sequência de ações, então o programa resultante 'Pn' é válido.

• Condição de Completude: Se 'P0' é válido e se 'P' é válido, então há alguma sequência de ações 'a1, ..., an' e programas correspondentes 'P1, ..., Pn' de modo que 'P1' resulta da ação 'a1' realizada em 'P0', resultados de 'P2' da execução da ação 'a2' em 'P1, ..., Pn' resulta da execução da ação 'an' em 'Pn-1' e 'P = Pn'.

Parafraseando a condição de solidez, afirma-se que: se alguém começa com um conjunto válido de condições 'on' e executa uma sequência de ações, então termina em uma situação válida.

Parafraseando a condição de completude, afirma-se que: dado qualquer primeiro arranjo válido de blocos, e qualquer segundo arranjo válido, deve haver alguma sequência de ações que podem ser executadas para trazer o segundo arranjo a partir do primeiro arranjo.

Exercício 2.19.4 Usando sua formulação de validade, podemos provar as condições de solidez e completude?

É possível dar uma formulação de transição de estado para as especificações de ação. Por exemplo, poderíamos considerar o estado inicial como o programa P0=(..., on(a,b),on(b,c),on(c,table)) (escrito como uma sequência) que tínhamos especificado anteriormente. As especificações de ação e outras cláusulas não variam. A execução de ações transforma um programa em outro. A função de transição 'T' pode ser expressa como

[math]T: P \times A \rightarrow P[/math]

onde 'P' se refere aos estados do programa e 'A' se refere às ações. As ações são os princípios básicos das cláusulas de especificação de ação. Por exemplo,

T(P0,r_put_on(b,a)) = P1

onde P1=(...,on(a,table),on(b,a),on(c,table),...), ou conforme a figura,

Fig. 2.19.3

Exercício 2.19.5 Começando com o mesmo 'P0' usado acima, desenhe um diagrama mostrando as transições que podem ser usadas para transformar 'P0' em P=(..., on(c,a),on(a,table),on(b,c),...). Identifique os estados intermediários do programa que são os resultados de ações individuais.

Exercício 2.19.6 Para os inclinados à matemática, formule definições mais cuidadosas para 'P' (os programas) e 'A' (as ações).

O Capítulo 7 tem mais informações sobre o uso do Prolog para criar especificações executáveis para protótipos de sistema, usando o método de especificação de ação.

Veja Também

• Código do Prolog para esta seção.
• Prolog Tutorial Sumário