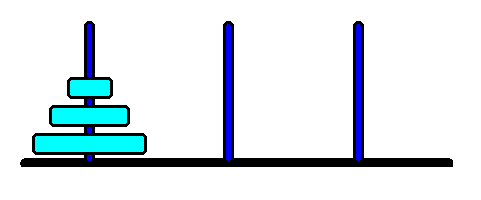
Quebra-cabeças das Torres de Hanói

O objetivo deste famoso quebra-cabeça é mover 'N' discos do pino esquerdo para o pino direito usando o pino central como um pino de fixação auxiliar. Em nenhum momento um disco maior pode ser colocado sobre um disco menor. O diagrama a seguir descreve a configuração inicial para 'N=3' discos.

Fig. 2.3

Aqui está um programa Prolog recursivo que resolve o quebra-cabeça. Consiste em duas cláusulas.

move(1,X,Y,_) :-  
    write('Move top disk from '), 
    write(X), 
    write(' to '), 
    write(Y), 
    nl. 
move(N,X,Y,Z) :- 
    N>1, 
    M is N-1, 
    move(M,X,Z,Y), 
    move(1,X,Y,_), 
    move(M,Z,Y,X).

As variáveis preenchidas por '_' (ou quaisquer variáveis que começam com sublinhado) são variáveis 'irrelevantes'. O Prolog permite que essas variáveis correspondam livremente a qualquer estrutura, mas nenhuma vinculação de variável resulta dessa correspondência gratuita.

Aqui está o que acontece quando Prolog resolve o caso 'N=3'.

?-  move(3,left,right,center). 
Move top disk from left to right 
Move top disk from left to center 
Move top disk from right to center 
Move top disk from left to right 
Move top disk from center to left 
Move top disk from center to right 
Move top disk from left to right 
 
yes

A primeira cláusula do programa descreve a movimentação de um único disco. A segunda cláusula declara como uma solução poderia ser obtida, recursivamente. Por exemplo, uma leitura declarativa da segunda cláusula para 'N=3', 'X=left', 'Y=right' e 'Z=center' equivale ao seguinte:

move(3,left,right,center) if
move(2,left,center,right) and ] *
move(1,left,right,center) and
move(2,center,right,left). ] **

Esta leitura declarativa da cláusula é obviamente correta. A leitura procedimental está intimamente relacionada à interpretação declarativa da cláusula recursiva. A interpretação processual seria mais ou menos assim:

Para satisfazer o objetivo ?- move(3,left,right,center) faça o seguinte:

satisfy the goal ?-move(2,left,center,right), and then
satisfy the goal ?-move(1,left,right,center), and then
satisfy the goal ?-move(2,center,right,left).

Além disso, poderíamos escrever as leituras declarativas para 'N=2':

move(2,left,center,right) if ] *
move(1,left,right,center) and
move(1,left,center,right) and
move(1,right,center,left).
move(2,center,right,left) if ] **
move(1,center,left,right) and
move(1,center,right,left) and
move(1,left,right,center).

Agora substitua os corpos dessas duas últimas implicações pelas cabeças e pode-se "ver" a solução que o objetivo do Prolog gera.

move(3,left,right,center) if
move(1,left,right,center) and
move(1,left,center,right) and *
move(1,right,center,left) and
---------------------------
move(1,left,right,center) and
---------------------------
move(1,center,left,right) and
move(1,center,right,left) and **
move(1,left,right,center).

Uma leitura procedimental para esta última grande implicação deveria ser óbvia. Este exemplo ilustra bem três operações principais do Prolog:

1) Os objetivos são comparados com o princípio da regra, e 2) o corpo da regra (com variáveis apropriadamente ligadas) torna-se uma nova sequência de objetivos, repetidamente,

até

3) algum objetivo básico ou condição é satisfeito, ou alguma ação simples é executada (como imprimir algo).

O processo de correspondência de variáveis é chamado de unificação.

Exercício 2.3.1 Desenhe uma árvore de cláusulas do programa para o objetivo move(3,left,right,center) para mostrar que é uma consequência do programa. Como esta árvore de cláusulas está relacionada ao processo de substituição explicado acima?

Exercício 2.3.2 Experimente o objetivo do Prolog ?-move(3,left,right,left). O que está errado? Sugira uma maneira de corrigir isso e prossiga para ver se a correção funciona.

Veja Também

• Código do Prolog para esta seção.
• 2.4 Carregando programas, editando programas
• Prolog Tutorial Sumário