Diagramas de estrutura e Prolog
Os diagramas considerados são grafos finitos cujos nós e arestas possuem um número finito de propriedades. A lógica computacional pode especificar diagramas e raciocinar sobre eles. A aparência visual de tal diagrama é expressa usando lógica factual. A lógica factual descreve a aparência factual de um diagrama específico. Propriedades gerais de objetos de diagrama e relacionamentos de ordem superior entre eles são representados na lógica genérica. A lógica genérica descreve os significados gerais que se pretende que certos tipos de diagramas tenham. Alguns exemplos são dados para motivar essa abordagem, incluindo algum código Prolog executável. Uma definição para a semelhança de significado de dois diagramas também é discutida brevemente.
Diagramas de estrutura (formulação matemática)
Os diagramas em consideração consistem em um número finito de nós e um número finito de arestas. Portanto, esse diagrama é um grafo finito. Cada aresta conecta dois nós (talvez o mesmo nó). Cada nó ou aresta possui um número finito de propriedades. As propriedades são especificadas usando um conjunto finito de chaves e um conjunto finito de valores. Suponha que o diagrama , tenha conjuntos de nós e arestas . O conjunto é definido pela união dos conjuntos e . é o conjunto de objetos no diagrama . Seja o conjunto finito de chaves (ou atributos) e seja o conjunto finito de valores que as chaves podem ter. A função de propriedade é
Esta função de propriedade atribui um valor a pares (objeto, chave). Na prática, pode ser uma função parcial (não definida para todos os pares). Por exemplo, a "cor da aresta 'e' é vermelha" pode ser representada como . De um modo geral, a equação
significa que o objeto de diagrama o tem valor de propriedade 'v' para a chave 'k'. Chaves e valores especificam atributos visuais dos objetos que aparecem nos diagramas.
Chamemos esses diagramas de diagramas de estrutura. Os diagramas de estrutura podem ser usados para representar a maioria das características salientes de muitos tipos de diagramas, incluindo diagramas de classe, diagramas de estado finito, fluxogramas, diagramas de rede, árvores decoradas, grafos decorados, diagramas de provas, árvores de provas e outros. No entanto, a definição provavelmente não pode representar adequadamente outros tipos de diagramas, como diagramas de Venn ou diagramas de Euler.
Diagramas de estrutura (formulação OO)
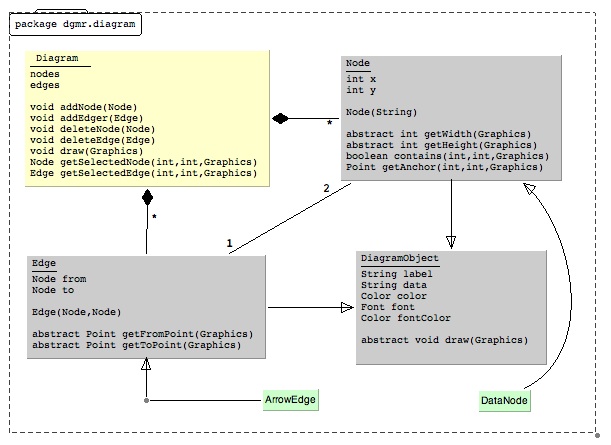
O diagrama da Figura 8.5.1 mostra um diagrama de classes orientado a objetos que descreve os relacionamentos entre diagramas, nós e arestas. Se alguém estiver familiarizado com esse tipo de diagrama, então seu significado é provavelmente bastante claro. É um diagrama de classes que caracteriza 'diagramas'. Este diagrama em particular pretende dizer que um 'diagrama' em geral possui nós e arestas; nós e arestas são tipos de objetos de diagrama que podem ter rótulos, cores, fontes, cores de fontes que podem se desenhar em um contexto gráfico. Os nós têm uma localização 'x' e 'y', e uma largura e altura calculadas. As arestas conectam dois nós. Além disso, existem tipos específicos de nós e arestas, como nós ovais ou arestas de linha, por exemplo.
Além disso, as classes que definem todos esses vários objetos pertencem a um pacote chamado 'dgmr.diagram'.
É possível usar muitos tipos de atributos (como cor, forma, fonte, etc.) para indicar algum significado em um diagrama. Por exemplo, as classes abstratas no diagrama são sombreadas em cinza para distingui-las das classes que podem ser instanciadas. A maioria dos diagramas de modelagem OO representaria esse relacionamento com uma tag <<abstract>>.
A Figura 8.5.1 representa um artefato de design para um sistema de software que foi usado pelo autor para desenhar o diagrama. O diagrama é um exemplo de trabalho útil para as seções a seguir.
A lógica factual dos diagramas de estrutura
A lógica factual de um diagrama descreve fatos sobre aquele diagrama específico. Primeiramente, esses são os fatos da aparência. Fatos de aparência descrevem a aparência do diagrama: rótulos, formas ou tipos de nós e arestas, conectividade de arestas, posição de nós, dimensões de nós, etc. Além disso, pode haver fatos de organização como declarações de nós ou arestas pertencentes a um diagrama particular. Para nossa estrutura de lógica factual, usamos expressões lógicas, ou cláusulas, com as seguintes formas de Prolog:
node(+Node)
edge(+Edge,+FromNode,+ToNode)
property(+Object,+Key,+Value)A primeira forma expressa que o nó pertence ou faz parte do diagrama. A segunda forma expressa que a aresta se conecta do 'nó1' ao 'nó2'. A terceira forma expressa que um objeto (nó ou aresta) possui um valor de propriedade para uma determinada chave. Essa estrutura é uma espécie de rede semântica.
Dada uma estrutura factual pretendida, as aparições dos diagramas são traduzidas em cláusulas factuais. O mais interessante são as traduções automáticas para a lógica usando um software que pode inspecionar os objetos do diagrama. Por exemplo, o software que desenhou o diagrama anterior possui um subsistema que gera código lógico factual. Esse software (escrito em Java) produz código semelhante ao seguinte código exemplo. Este código exemplo expressa alguns dos fatos sobre o diagrama anterior. O abundante código real produzido (arquivo diagram.pl) é mostrado reformatado (e simplificado) para exibição aqui, e uma grande parte dele foi omitida.
% nodes
node(node_0) .
...
% edges
edge(edge_0,node_1,node_2).
...
% property key = label
property(node_0,label,'Diagram').
...
% property key = type
property(node_0,type,'dgmr.diagram.DataNode').
...
% property key = color
property(node_0,color,[255,255,255]).
...
% property key = position
property(node_0,position,[38,55]).O gerador de código lógico usou os valores das variáveis de instância do objeto e o conceito de introspecção Java para gerar a lógica factual. Se os diagramas tiverem conteúdo mais generalizado, como imagens, os valores de certas chaves precisam ser links para esse conteúdo ou algum outro descritor.
Que tipo de especificação lógica é razoável usar? Nesta seção, usamos o código que pode ser calculado no estado em que se encontra com o Prolog ou pode ser carregado em um meta-interpretador lógico do Prolog. Outras formulações semelhantes podem ser apropriadas para uso com meta-interpretadores lógicos de Prolog especializados.
A lógica genérica dos diagramas de estrutura
A lógica genérica descreve todos os significados pretendidos ou gerais sobre uma classe de diagramas relacionados. Isso é feito especificando regras que definem os conceitos pretendidos. As regras genéricas se aplicam a uma coleção de diagramas em uma área particular de aplicação.
Para obter um exemplo específico, considere o conceito de herança em um diagrama de hierarquia de classes orientado a objetos. O tipo usual de regra para representar esse relacionamento em diagrama é desenhar um certo tipo de aresta terminal (geralmente algum tipo de seta com a ponta aberta) da classe filha para a classe pai (com links de linha intermediária da classe filha permitida). Essa convenção geral se aplica a todos os diagramas de hierarquia. Segue um código exemplo (arquivo extends.pl) para calcular a relação de herança. Essa base de regra genérica é adequada para combinação com as regras factuais que possuem os formatos de predicado fornecidos.
%% class S extends class P
extends(S,P) :-
node(NS),
classNode(NS),
property(NS,'label',S),
node(NP),
classNode(NP),
property(NP,'label',P),
connectedByArrow(NS,NP).
%% class S extends class P, Nth removed
extends(S,P,1) :-
extends(S,P).
extends(S,P,N) :-
extends(S,M),
extends(M,P,N1),
N is N1+1.
%% Is there an "extends" edge between X and Y?
connectedByArrow(X,Y) :-
edge(E,X,Y),
closedArrow(E).
connectedByArrow(X,Y) :-
edge(E,X,C),
property(C,'type','dgmr.diagram.ConnectorNode'),
lineEdge(E),
connectedByArrow(C,Y).
%% Definition of "closed arrow" edge
closedArrow(E) :-
( property(E,'type','dgmr.diagram.ArrowEdge') |
property(E,'type','dgmr.diagram.CubicEdge') ),
property(E,'tip','closed_tip').
%% Definition of "line" edge
lineEdge(E) :-
( property(E,'type','dgmr.diagram.ArrowEdge') |
property(E,'type','dgmr.diagram.CubicEdge') ),
property(E,'tip','no_tip').
%% Definition of "class" node
classNode(N) :-
property(N,'type','dgmr.diagram.DataNode') |
property(N,'type','dgmr.diagram.RectNode').Se a lógica factual (arquivo diagram.pl gerado para o diagrama na Figura 8.5.1) e esta base de regra genérica (arquivo extends.pl) forem carregados no mesmo contexto do Prolog, então o seguinte mostra as respostas extraídas pelo Prolog.
?- [diagram,extends]. % load these two files
% diagram compiled 0.00 sec, 20,760 bytes
% extends compiled 0.00 sec, 2,200 bytes
?- extends(X,Y). % DIRECT EXTENSION
X = 'Edge'
Y = 'DiagramObject' ;
X = 'Node'
Y = 'DiagramObject' ;
X = 'ArrowEdge'
Y = 'Edge' ;
X = 'DataNode'
Y = 'Node' ;
No
?- extends(X,Y,N). % DIRECT or INDIRECT EXTENSION
X = 'Edge'
Y = 'DiagramObject'
N = 1 ;
X = 'Node'
Y = 'DiagramObject'
N = 1 ;
X = 'ArrowEdge'
Y = 'Edge'
N = 1 ;
X = 'DataNode'
Y = 'Node'
N = 1 ;
X = 'ArrowEdge'
Y = 'DiagramObject'
N = 2 ;
X = 'DataNode'
Y = 'DiagramObject'
N = 2 ;
No
?-As respostas produzidas indicam primeiras relações de herança uma vez removidas ('X' herda de 'Y' diretamente) e, em seguida, relações de herança removidas duas vezes ('X' herda de algum 'W' que por sua vez herda de 'Y'), e assim por diante.
Observe que extends(-,-,-) pode ser usado para calcular uma métrica de software orientada a objeto: O "diâmetro de herança" de um sistema, que é o caminho de herança mais longo para qualquer objeto no sistema (quão removida a herança poderia ser). Essa modificação é um exercício para o leitor.
Exercício 8.5.1. Implemente esta métrica de diâmetro de herança.
No exemplo atual, herança, é um pouco mais complicado do que o leitor casual pode apreciar à primeira vista. A apresentação até este ponto depende da suposição razoável de que o criador do diagrama humano desenhou bordas de linha na direção de uma seta de herança. Por exemplo, a borda da linha na Figura 8.5.1 foi desenhada a partir do nó rotulado como "ArrowEdge" para o pequeno nó do conector redondo (e não na direção reversa. Caso esta borda da linha tivesse sido desenhada na direção oposta, ninguém poderia ver a diferença visualmente. O diagrama teria exatamente a mesma aparência. Mas a lógica factual não teria informações suficientes para produzir uma conclusão de herança (X = 'ArrowEdge', Y = 'DiagramObject'). Se nossa intenção fosse para permitir que as bordas da linha de conexão fossem desenhadas em qualquer direção, não poderíamos usar um programa Prolog simples para interpretar nossa base de fatos (infelizmente!).
Exercise 8.5.2. Show how to modify extends.pl so that the line edges to the connector nodes could be drawn in either direction. (Hint: only one line needs change.)
Algumas intenções podem ser deduzidas da conectividade geral dos nós, como o exemplo de herança que acabamos de dar. Outras intenções podem usar outros fatos da base de regra factual. Por exemplo, "pertencer ao pacote" no diagrama anterior poderia ser calculado usando as posições reais dos nós (onde eles estão localizados na visualização), em relação ao visual de "pacote tracejado". Ainda outras intenções podem ser baseadas no conteúdo textual (ou outro) associado a um nó, como os campos, construtores ou métodos de um nó de classe, ou com notas de restrição anexadas aos mesmos itens. Acreditamos que a lógica de resolução usando cláusulas definidas deve ser suficiente para grande parte da lógica de especificação. No entanto, é necessário cuidado ao escrever essas especificações do Prolog de modo a evitar definições de grafos cíclicos que causariam recursão infinita durante as consultas.
Exercício 8.5.3. (Grande projeto) Projete e implemente um programa Prolog que seja capaz de analisar um site e criar um diagrama para seu conteúdo. Projete uma lógica genérica para analisar o conteúdo de um site por meio da análise de seu diagrama e construa o mecanismo de consulta para isso. É uma espécie de sistema especialista para a web semântica.
Os significados dos diagramas de estrutura
Falando logicamente, qual é o significado de um diagrama de estrutura? A definição a seguir usa a teoria da programação lógica. Veja a referência Lloyd (1984, 1987)[1].
Suponha que a base de regra factual consiste em cláusulas unitárias (conforme descrito anteriormente) e que a base de regra genérica é um programa de registro de dados (cláusulas definidas positivas, sem negação e sem predicados internos como sequências ou listas). O significado do diagrama correspondente aos fatos e às regras genéricas é definido como o modelo mínimo das bases de regra combinadas .
Suponha que seja o conjunto de todas as instâncias de regras em que foram baseadas em termos gerados pelas constantes e símbolos de função de . O modelo mínimo pode ser definido indutivamente como segue.
contém apenas fatos . Para definimos...
Cada contém todas as consequências derivadas usando regras em e consequências derivadas de , para .
Finalmente,
Observe novamente que esse modelo mínimo sempre contém a base de regra factual.
Usando uma base de regra genérica comum , dois diagramas e têm o mesmo significado pretendido fornecido
onde é a base de regra extensional determinada por e é a base de regra extensional determinada por (e onde "\" denota diferença de conjunto). Falando intuitivamente: os dois diagramas têm o mesmo significado pretendido, desde que tenham as mesmas consequências, embora possam ter aparências um tanto diferentes (factuais).
Por exemplo, no exemplo de herança anterior, está claro que o significado do diagrama não deve mudar se alguns dos nós forem movidos um pouco. Dizemos "um pouco" porque poderíamos facilmente embaralhar a aparência visual e, assim, perder o impacto visual, quanto mais o significado intuitivo. Obviamente, se dependesse estritamente da posição, os nós não poderiam ser movidos muito antes que o significado pretendido do diagrama mudasse.
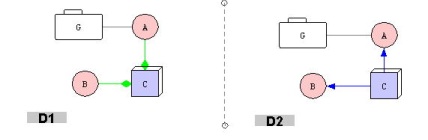
Para o exemplo a seguir, consulte a Figura 8.5.2. Suponha que em um certo tipo de diagrama algumas intenções (regras) sejam especificadas em para as arestas do diamante que são verdes. Suponha que consideremos todas as outras intensões iguais, mas que agora as bordas de setas sólidas em azul são usadas em todos os lugares para especificar o que antes era indicado para bordas de losangos verdes, dando novas intenções . Suponha ainda que os diagramas e sejam iguais, exceto que sempre que tiver bordas de losango verdes, terá bordas de setas sólidas azuis. Então, faz sentido dizer que e têm o mesmo significado.
Uma caracterização matemática é a seguinte. Suponha que e sejam diagramas com regras genéricas e e suponha que haja uma função de analogia um-para-um
que mapeia as especificações do nó para as especificações do nó correspondente, as especificações de aresta para as especificações de arestas correspondentes e as especificações de propriedade para as especificações de propriedade correspondentes. Então dizemos que a analogia a atribui o mesmo significado a e desde
Exercício 8.5.4 Anteriormente nesta seção, fornecemos uma metáfora gráfica alternativa para classes abstratas. Dissemos que um nó de classe com uma cor cinza poderia ser usado para significar que a classe era uma classe abstrata. Dissemos que uma maneira alternativa de representar classes abstratas era usar um rótulo <<abstract>> em algum lugar da especificação diagramática (por exemplo, UML). Como as definições nesta subseção cobrem este conceito específico? Qual é a função de analogia?
Exercício 8.5.5. (Projeto) Implemente funções de analogia de uma maneira geral para que os diagramas possam ser computados como tendo o mesmo significado.
Esta breve discussão evitou muitos detalhes técnicos. Os conceitos parecem muito teóricos, mas podem ser de considerável importância prática.
Além disso, se não é um programa lógico datalog simples, então deve-se definir o significado em termos de alguma outra semântica de programa lógico. Por exemplo, se contiver regras com negação (destinadas a serem computadas como negação como falha), poderíamos usar algum tipo de semântica de mundo fechado. Consulte a referência Lloyd (1984, 1987)[1] novamente. Essa semântica é não monotônica, o que no contexto atual dos diagramas significa que algumas conclusões sobre os diagramas podem ser bloqueadas pela adição de novos nós, arestas ou propriedades.
Por exemplo, suponha que temos uma regra que diz que uma determinada conclusão é válida, desde que algum nó envolvido não seja azul. Se essa conclusão for válida para um determinado diagrama e mudarmos a cor do nó crucial para azul, a conclusão se tornará falsa. Isso nunca acontece para a lógica definida positiva. Outras lógicas (digamos, a possibilidade de fatos com negação clássica explícita e regras contendo as mesmas) exigiriam outra semântica apropriada.
Pode haver melhores lógicas para calcular as consequências dos diagramas.
Prolog code: