Meta-interpretadores no Prolog

De Augusto Baffa Wiki
Revisão de 01h05min de 2 de novembro de 2020 por Abaffa (discussão | contribs) (Criou página com 'Os programas também podem ser considerados como dados de entrada para outros programas. Os programas Prolog são sequências de termos prolog, portanto, os programas prolog s...')
(dif) ← Edição anterior | Revisão atual (dif) | Versão posterior → (dif)
Ir para navegação Ir para pesquisar

Os programas também podem ser considerados como dados de entrada para outros programas. Os programas Prolog são sequências de termos prolog, portanto, os programas prolog servem facilmente como dados de entrada. Um meta-interpretador de Prolog usa dados de programa como base para cálculos adicionais. Nesta seção, são discutidos vários meta-interpretadores prolog que modificam o cálculo dos objetivos do prolog.

O Capítulo 6 estuda alguns meta-interpretadores de prólogo para lógica.

Meta-interpretador Prolog Simples

O programa a seguir especifica um interpretador de árvores de cláusulas no Prolog 

clause_tree(true) :- !.      /* true leaf */ 
clause_tree((G,R)) :- 
   !, 
   clause_tree(G),
   clause_tree(R).           /* search each branch */ 
clause_tree(G) :- 
   clause(G,Body),
   clause_tree(Body).        /* grow branches */

Para ilustrar como esse meta-interpretador funciona, vamos usá-lo para interpretar o programa para 'member': 

member(X,[X|_]). 
member(X,[_|R]) :- member(X,R).

Considere o objetivo... 

?- clause_tree(member(X,[a,b,c]). 
X = a ; 
X = b ; 
X = c ; 
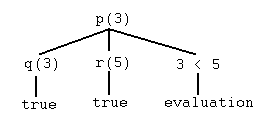
no

Assim, o meta-interpretador cria árvores de cláusulas e encontra as mesmas respostas que o próprio Prolog calcularia. Aqui está uma árvore de cláusulas do programa enraizada em 'clause_tree(membr(b,[a,b,c]))':

Fig. 3.3.1

Usando avaliação para objetivos integrados

Pode-se adicionar avaliação ao programa 'clause_tree'. A maneira como isso é feito depende do tipo de Prolog que se está usando. 

clause_tree(true) :- !.
clause_tree((G,R)) :-
   !,
   clause_tree(G), 
   clause_tree(R).
clause_tree(G) :- 
   (predicate_property(G,built_in) ;  
     predicate_property(G,compiled) ), 
   call(G).              %% let Prolog do it
clause_tree(G) :- clause(G,Body), clause_tree(Body).

A nova terceira cláusula diz que se o objetivo G for incorporado (por exemplo, aritmética), então chama-se o objetivo Prolog subjacente para fazer a avaliação; e da mesma forma se G for compilado na memória. Então, por exemplo, com a nova definição... 

?- clause_tree((X is 3, X <  5)). 
X = 3

Detecção de Loop

Meta-interpretadores são muito úteis para redesenhar os mecanismos de controle do Prolog. Por exemplo, considere o seguinte programa: 

p :- q. 
q :- p. 
p :- r. 
r.

Se alguém tentar o objetivo do Prolog ?-p., as duas primeiras cláusulas seriam a causa do loop infinito, como na derivação a seguir

Fig. 3.3.2

No entanto, r, p e q são consequências do programa. Desenhe uma árvore de cláusulas do programa com raiz em r, p e q, respectivamente, para demonstrar que cada uma é uma consequência. O fato de que Prolog não pode calcular essas consequências é um exemplo da incompletude do Prolog. Para o bem da eficiência geral da programação, Prolog não tenta detectar nenhum loop. Há também uma limitação teórica: Não existe um algoritmo geral de detecção de loop que pudesse ser aplicado ao Prolog e que teria sucesso na detecção de todos os loops. Se houvesse, teria de fato resolvido o problema da parada.

No entanto, ainda é um problema muito interessante tentar detectar alguns loops. Aqui está uma modificação do programa 'clause_tree/1' que pode detectar alguns loops: 

clause_tree(true,_) :- !. 
clause_tree((G,R),Trail) :-
   !, 
   clause_tree(G,Trail),
   clause_tree(R,Trail). 
clause_tree(G,Trail) :-
   loop_detect(G,Trail),
   !, 
   fail.
clause_tree(G,Trail) :- 
   clause(G,Body), 
   clause_tree(Body,[G|Trail]).

loop_detect(G,[G1,_]) :- G == G1.
loop_detect(G,[_,R])  :- loop_detect(G,R).

Adicionamos um parâmetro Trail ao meta-interpretador e um 'loop_detect'. É instrutivo comparar este programa com o programa de pesquisa na seção 2.13. Agora temos... 

?- clause_tree(p,[]). 
yes

A terceira cláusula "captura" o loop e permite que a outra escolha p :- r seja tentada.


Desenhando árvores de cláusulas

Agora considere a seguinte modificação do programa. Essa versão também gera um valor de parâmetro de árvore de cláusulas ao interpretar um programa. 

clause_tree(true,_,true) :- !. 
clause_tree((G,R),Trail,(TG,TR)) :-
   !, 
   clause_tree(G,Trail,TG),
   clause_tree(R,Trail,TR). 
clause_tree(G,_,prolog(G)) :- 
   (predicate_property(G,built_in) ;  
     predicate_property(G,compiled) ), 
   call(G).              %% let Prolog do it
clause_tree(G,Trail,_) :-
   loop_detect(G,Trail),
   !, 
   fail.
clause_tree(G,Trail,tree(G,T)) :- 
   clause(G,Body), 
   clause_tree(Body,[G|Trail],T).

Carregue este último programa e o programa de teste simples... 

p(X) :- q(X), r(Y), X < Y.
q(3).
r(2).
r(5).
r(10).

... e depois chame o seguinte objetivo ... 

?- clause_tree(p(X),[],Tree)

Tree = tree(p(3),(tree(q(3),true),tree(r(5),true),prolog(3 < 5)))
X = 3 ;

Tree = tree(p(3),(tree(q(3),true),tree(r(10),true),prolog(3 < 10)))
X = 3 ;

No

Segue um programa para desenhar a árvore de cláusulas que é gerada ... 

why(G) :- clause_tree(G,[],T),
          nl,
          draw_tree(T,5).

draw_tree(tree(Root,Branches),Tab) :- !,
   tab(Tab),
   write('|-- '),
   write(Root),
   nl,
   Tab5 is Tab + 5,
   draw_tree(Branches,Tab5).
draw_tree((B,Bs),Tab) :- !,
   draw_tree(B,Tab),
   draw_tree(Bs,Tab).
draw_tree(Node,Tab) :-
   tab(Tab),
   write('|-- '),
   write(Node),
   nl.

Agora, interpretando o mesmo programa de amostra acima ... 

?- why(p(X)).

   |-- p(3)
        |-- q(3)
             |-- true
        |-- r(5)
             |-- true
        |-- prolog(3 <  5)

X = 3 ;

   |-- p(3)
        |-- q(3)
             |-- true
        |-- r(10)
             |-- true
        |-- prolog(3 <  10)
   
X = 3 ;

No

A árvore correspondente à primeira resposta seria desenhada ("orientada verticalmente") como se segue ...

Fig. 3.3.3

Aprofundamento iterativo

Para motivar o último tópico desta seção, considere o seguinte programa "mal-implementado": 

connected(X,Y) :- connected(X,Z), connected(Z,Y).
connected(1,2).
connected(2,3).
connected(3,4).
connected(4,5).

Se alguém tentar chamar o 'connected' usando Prolog, haverá um problema com "recursão à esquerda". Por exemplo, 

?- connected(1,2).
 ...

Esse objetivo faz com que Prolog entre em uma descida infinita de sub-objetivos. (Tente você mesmo!) Claro, poderíamos ter evitado isso -- para esse objetivo -- se tivéssemos colocado a "regra" após os "fatos" no programa 'mal-implementado'. Mas, mesmo com essa mudança, um objetivo como '?- connected(1,What)' teria causado um problema se forçamos um backtracking para tentar encontrar todas as soluções. (Novamente, tente você mesmo.)

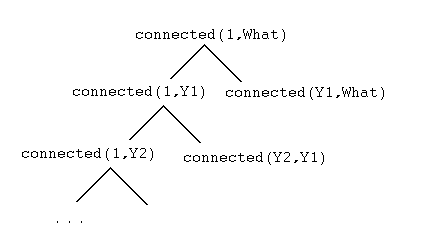
O loop aqui não é como o loop discutido acima. Para explicar isso, considere o programa "mal-implementado" original e considere a árvore de derivação do Prolog gerada ao tentar o objetivo '?- connected(1,What)'

Fig. 3.3.4

Deve ficar claro na Fig. 3.3.4 que o problema realmente não está no loop de uma maneira que repete um objetivo, embora a mesma cláusula seja usada repetidamente. A própria regra 'connected' não sabe quantos links pode haver entre '1' e 'What', então pode-se dizer que essa regra está (por si só) tentando permitir que haja 1 link, 2 links, 3 links, ..., etc. Isso às vezes é chamado de loop de previsão. A verificação do loop anterior tentou detectar um objetivo repetido que era "equivalente" a um objetivo anterior (ou idêntico ao objetivo anterior). O comportamento repetitivo atual não está realmente gerando objetivoss que sejam "totalmente equivalentes" aos objetivos anteriores.

Um método para evitar esse tipo de descida infinita é chamado de "aprofundamento iterativo", o que significa que ainda se usa a busca em profundidade, mas se busca "iterativamente" até uma certa profundidade, depois mais fundo, depois ainda mais fundo, ..., etc. . Aqui está um meta-interpretador que faz isso. Este meta-interpretador é bastante semelhante aos anteriores. No entanto, este tem apenas dois parâmetros extras: um para a profundidade atual de um objetivo e outro para o limite de profundidade atual. Este interpretador não faz o tipo anterior de verificação de loop nem gera a árvore simbólica, mas chama Prolog para objetivos de avaliação. (Claro, esses recursos poderiam ser facilmente adicionados, mas aqui nos concentramos apenas no conceito de aprofundamento iterativo.) 

clause_tree(true,_,_) :- !.
clause_tree(_,D,Limit) :- D > Limit, 
                          !, 
                          fail.  %% reached depth limit
clause_tree((A,B),D,Limit) :- !, 
                              clause_tree(A,D,Limit), 
                              clause_tree(B,D,Limit).
clause_tree(A,_,_) :- predicate_property(A,built_in),
                      !,
                      call(A).
clause_tree(A,D,Limit) :- clause(A,B),
                          D1 is D+1, 
                          clause_tree(B,D1,Limit).

iterative_deepening(G,D) :- clause_tree(G,0,D).
iterative_deepening(G,D) :- write('limit='),
                            write(D),
                            write('(Hit Enter to Continue.)'),
                            get0(C),
                            ( C == 10 ->
                                 D1 is D + 5,
                                 iterative_deepening(G,D1)  ).

Observe que o interpretador pretendido é 'iterative_deepening(+Goal,+InitDepth)' onde '+Goal' pode, é claro, conter variáveis. Este meta-interpretador de aprofundamento iterativo usa "estágios": a profundidade do primeiro estágio é '+InitDepth', o segundo estágio vai para a profundidade 'InitDepth+5', etc.

Agora, suponha que este programa e o programa 'connected' original tenham sido carregados. O que acontece desta vez? ... 

?- iterative_deepening(connected(1,What), 1).
What=3 ;
What=2 ;
Limit=1(Hit Enter to Continue)
What=5 ;
What=5 ;
What=5 ;
What=4 ;
What=5 ;
What=5 ;
What=4 ;
What=3 ;
What=2 ;
Limit=6(Hit Enter to Continue.)
What=5                           %% stop

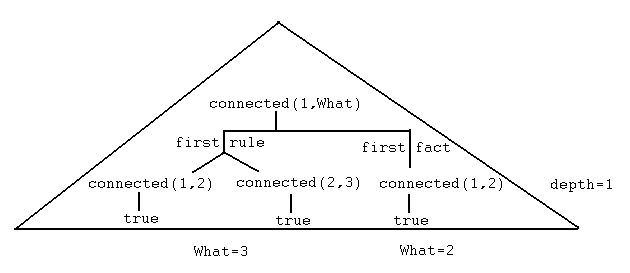
Yes

Observe como o meta-interpretador 'iterative_deepening' primeiro encontra soluções que estão próximas do limite de profundidade atual e, em seguida, prossegue para descobrir soluções mais rasas. Uma boa descrição gráfica desse fenômeno é que o meta-interpretador busca o canto esquerdo inferior de um triângulo de profundidade igual ao limite de profundidade atual e, em seguida, busca profundidades mais rasas na parte direita do triângulo, conforme sugerido pelo diagrama a seguir. O diagrama mostra soluções para 'connected(1,What)' que são "acessíveis" na profundidade 1, que foi o primeiro estágio para o objetivo acima.

Fig. 3.3.5

Teoricamente, o aprofundamento iterativo tem um tipo de comportamento ideal para busca "cega": o aprofundamento iterativo encontrará qualquer solução possível em um estágio profundo o suficiente para incluir a árvore de cláusulas que justifica essa solução -- espaço O(d), d=profundidade -- em tempo O(b**d), b=fator de ramificação médio. Outros tipos de busca completa, como na busca em largura (ou ampliação iterativa), precisam buscar em um número esperado maior de nós.


Esta seção sobre meta-interpretadores serve como uma introdução aos meta-interpretadores mais elaborados discutidos no capítulo 6 do Prolog Tutorial.


Exercício 3.3.1 Desenhe uma árvore de derivação Prolog para 'clause_tree(p,[])' para mostrar como 'clause_tree/2' captura o loop.


Exercício 3.3.2 Considere o programa 

p(a) :- p(X). 
p(b).

Mostre que 'clause_tree/2' acima não detectará o loop para este programa. Você pode redesenhar a verificação de loop para que o loop neste exemplo seja interrompido?

O segundo exercício mostra que pode ser difícil detectar tipos específicos de loops (além da impossibilidade de detectar todos os loops).


Exercício 3.3.3 O meta-interpretador 'clause_tree' desenvolve árvores de cláusulas do programa. Ele não modela (exatamente) árvores de derivação do Prolog! Explique por quê. Dica: Observe que as árvores de derivação do Prolog têm nós que são sequências de literais. Projete um meta-interpretador Prolog, semelhante ao do início desta seção, mas cujos nós sejam sequências de sub-objetivos. Este novo interpretador é equivalente ao desta seção? (Defina o que equivalente significaria primeiro.) Implemente a verificação de loop para este meta-interpretador.

Veja Também

Disponível em “http://www.augustobaffa.pro.br/wiki/index.php?title=Meta-interpretadores_no_Prolog&oldid=200”