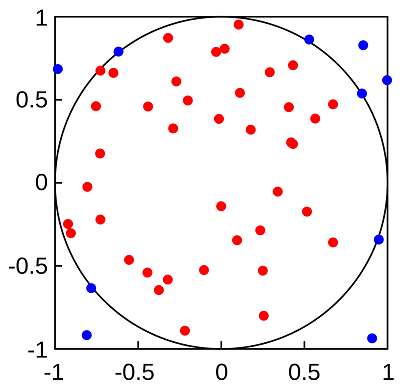
Estimating PI with Monte Carlo

Os algoritmos de Monte Carlo tentam estimar por meio de amostragem aleatória, pois o cálculo do valor real pode levar muito tempo. Monte Carlo faz uso de amostras aleatórias para gerar uma boa estimativa. Existem muitas técnicas diferentes de Monte Carlo, algumas das quais são híbridas entre Monte Carlo e outras técnicas (Robert, 2005).

Um exemplo simples de Monte Carlo é sua estimativa do valor de PI

Agora colocaremos pontos aleatórios dentro do quadrado e do círculo. A proporção de pontos internos e externos nos dirá o valor de PI. A área do quadrado é o comprimento multiplicado pela largura. Como um quadrado tem a mesma largura que o comprimento, a área do quadrado é essencialmente a largura vezes ela mesma, ou largura ao quadrado.

A área de um círculo é PI vezes seu raio ao quadrado. O diâmetro do círculo é igual à largura do quadrado. Vamos calcular a razão da área do círculo para o quadrado usando a equação abaixo.

[math] p = \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4}[/math]

A largura do quadrado é igual a duas vezes o raio do círculo. Portanto, podemos descrever o diâmetro do quadrado como duas vezes o raio ao quadrado. Tomaremos a proporção de pontos dentro do círculo para fora e multiplicaremos por 4. Isso nos dará uma aproximação de PI.

Exemplo em Python

Exemplo de sorteios

def estimate_pi(times = 10000, seed1=None, seed2=None):
    tries=0
    success=0

    # pick a point at random.
    if seed1 == None:
        t = time.perf_counter()
        seed1 = int(10**9*float(str(t-int(t))[0:]))
    x = pseudo_uniform(seed=seed1, size=times)

    if seed2 == None:
        t = time.perf_counter()
        seed2 = int(10**9*float(str(t-int(t))[0:]))
    y = pseudo_uniform(seed=seed2, size=times)

    for i in range(times):
        tries += 1

        # was the point inside of a circle?
        if x[i] * x[i] + y[i] * y[i] <= 1:
            success += 1
            
    pi = 4 * success / tries
    
    return pi

Exemplo:

import math

est_pi = estimate_pi(10000000, 123456789, 987654321)

print("Estimated PI: %f" % est_pi)
print("Real PI: %f" % math.pi)
print("Error: %f" % abs(est_pi - math.pi))

Estimated PI: 3.142123

Real PI: 3.141593

Error: 0.000531

Veja Também

• Gerador Aleatório Uniforme