Estimating PI with Monte Carlo

Monte Carlo algorithms attempt to estimate through random sampling, as it can be time intensive to calculate the actual value. Monte Carlo makes use of random samples to generate a good estimate. There are many different Monte Carlo techniques, some of which are hybrids between Monte Carlo and other techniques. (Robert, 2005)

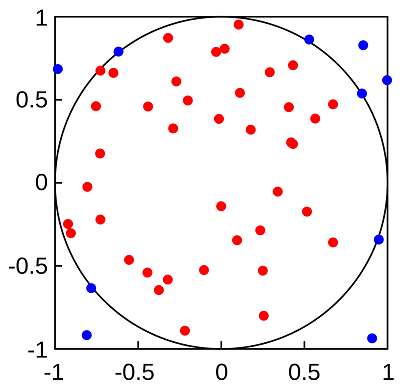
One simple example of Monte Carlo is its estimation of the value of PI

We will now place random points inside of the square and circle. The ratio of points inside to outside will tell us the value of PI. The area of the square is its length multiplied by its width. Because a square has the same width as length, the area of the square is essentially the width times itself, or width squared.

A circle’s area is PI times its radius squared. The diameter of the circle is the same as the width of the square. We will calculate the ratio of the area of the circle to the square by using Equation below.

[math] p = \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4}[/math]

The width of the square is the same as two times the circle’s radius. So we can describe the square’s diameter as two times the radius squared. We will take the ratio of points inside the circle to outside and multiply by 4. This will give us an approximation of PI.

Exemplo em Python

Attempts sample

def estimate_pi(times = 10000, seed1=None, seed2=None):
    tries=0
    success=0

    # pick a point at random.
    if seed1 == None:
        t = time.perf_counter()
        seed1 = int(10**9*float(str(t-int(t))[0:]))
    x = pseudo_uniform(seed=seed1, size=times)

    if seed2 == None:
        t = time.perf_counter()
        seed2 = int(10**9*float(str(t-int(t))[0:]))
    y = pseudo_uniform(seed=seed2, size=times)

    for i in range(times):
        tries += 1

        # was the point inside of a circle?
        if x[i] * x[i] + y[i] * y[i] <= 1:
            success += 1
            
    pi = 4 * success / tries
    
    return pi

Example:

import math

est_pi = estimate_pi(10000000, 123456789, 987654321)

print("Estimated PI: %f" % est_pi)
print("Real PI: %f" % math.pi)
print("Error: %f" % abs(est_pi - math.pi))

Estimated PI: 3.142123

Real PI: 3.141593

Error: 0.000531

See also

• Gerador Aleatório Uniforme