Coloração de mapas

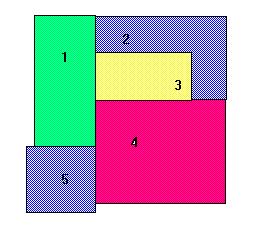
Um famoso problema da matemática diz respeito à coloração de regiões planas adjacentes. Como os mapas cartográficos, é necessário que, quaisquer que sejam as cores realmente usadas, duas regiões adjacentes não podem ter a mesma cor. Duas regiões são consideradas adjacentes, desde que compartilhem algum segmento de linha de limite. Considere o seguinte mapa.

Fig. 2.1.1

Nós numeramos as regiões. Para representar quais regiões são adjacentes, considere também o gráfico a seguir.

Fig. 2.1.2

Aqui, apagamos os limites originais e, em vez disso, desenhamos um arco entre os nomes de duas regiões, desde que fossem adjacentes no desenho original. Na verdade, o grafo de adjacência transmitirá todas as informações originais de adjacência. Uma representação Prolog para as informações de adjacência pode ser representada pelas seguintes cláusulas de unidade, ou fatos.

adjacent(1,2).         adjacent(2,1). 
adjacent(1,3).         adjacent(3,1). 
adjacent(1,4).         adjacent(4,1). 
adjacent(1,5).         adjacent(5,1). 
adjacent(2,3).         adjacent(3,2). 
adjacent(2,4).         adjacent(4,2). 
adjacent(3,4).         adjacent(4,3). 
adjacent(4,5).         adjacent(5,4).

Se essas cláusulas fossem carregadas no Prolog, poderíamos observar o seguinte comportamento para alguns objetivos.

?- adjacent(2,3). 
yes 
?- adjacent(5,3). 
no 
?- adjacent(3,R). 
R = 1 ; 
R = 2 ; 
R = 4 ; 
no

Pode-se declarar colorações para as regiões no Prolog também usando cláusulas unitárias.

color(1,red,a).    color(1,red,b). 
color(2,blue,a).   color(2,blue,b). 
color(3,green,a).  color(3,green,b). 
color(4,yellow,a). color(4,blue,b). 
color(5,blue,a).   color(5,green,b).

Aqui, codificamos as cores 'a' e 'b'. Queremos escrever uma definição Prolog de uma coloração conflitante, o que significa que duas regiões adjacentes têm a mesma cor. Por exemplo, aqui está uma cláusula Prolog ou regra para esse efeito.

conflict(Coloring) :- 
   adjacent(X,Y), 
   color(X,Color,Coloring), 
   color(Y,Color,Coloring).

Por exemplo,

?- conflict(a). 
no 
?- conflict(b). 
yes 
?- conflict(Which). 
Which = b

Aqui está outra versão de 'conflito' que possui parâmetros mais lógicos.

conflict(R1,R2,Coloring) :- 
   adjacent(R1,R2), 
   color(R1,Color,Coloring), 
   color(R2,Color,Coloring).

O Prolog permite e distingue as duas definições de 'conflict'; um tem um parâmetro lógico ('conflict/1') e o outro tem três ('conflict/3'). Agora temos...

?- conflict(R1,R2,b). 
R1 = 2   R2 = 4 
?- conflict(R1,R2,b),color(R1,C,b). 
R1 = 2   R2 = 4   C = blue

O último objetivo significa que as regiões 2 e 4 são adjacentes e ambas são azuis. Instâncias aterradas como 'conflict(2,4,b)' são consideradas consequências do programa Prolog. Uma maneira de demonstrar tal consequência é desenhar uma árvore de cláusulas do programa tendo como consequência a raiz da árvore, usar cláusulas do programa para ramificar a árvore e, eventualmente, produzir uma árvore finita com todas as folhas verdadeiras. Por exemplo, a seguinte árvore de cláusulas pode ser construída usando instâncias totalmente fundamentadas (sem variáveis) de cláusulas do programa.

Fig. 2.1.3

O ramo inferior esquerdo desenhado na árvore corresponde à cláusula de unidade

adjacent(2,4).

que é equivalente em Prolog à cláusula

adjacent(2,4) :- true.

Agora, por outro lado, 'conflict(1,3,b)' não é uma consequência do programa Prolog porque não é possível construir uma árvore de cláusulas finitas usando cláusulas fundadas de 'P' contendo todas as folhas 'verdadeiras'. Da mesma forma, 'conflict(a)' não é uma consequência do programa, como seria de se esperar. Teremos mais a dizer sobre as árvores de cláusulas do programa nas seções subsequentes.

Iremos revisitar o problema de coloração novamente na Seção 2.9, onde desenvolveremos um programa Prolog que pode computar todas as colorações possíveis (com as cores dadas). A famosa conjectura das quatro cores era que nenhum mapa planar requer mais do que quatro cores diferentes. Isso foi provado por Appel e Haken (1976). A solução utilizou um programa de computador (não Prolog) para verificar muitos casos específicos de mapas planares, a fim de descartar possíveis casos problemáticos. O mapa da Fig. 2.1.1 requer pelo menos quatro cores; por exemplo ...

Fig. 2.1.4

Exercício 2.1 Em um mapa com N regiões, estime quantos cálculos podem ser necessários para determinar se a coloração está ou não em conflito. Argumente usando árvores de cláusulas do programa.

Veja Também

• Código do Prolog para esta seção.
• 2.2 Duas Definições de Fatorial
• 2.9 Redux da coloração de mapas
• Prolog Tutorial Sumário