Estruturas e caminhos em grafos em Prolog

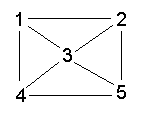
Como exemplo, considere o seguinte grafo conectado:

Fig. 2.15

As arestas podem ser representadas no Prolog como fatos:

edge(1,2).
edge(1,4).
edge(1,3).
edge(2,3).
edge(2,5).
edge(3,4).
edge(3,5).
edge(4,5).

Para representar o fato de que as arestas são bidirecionais, poderíamos adicionar mais oito cláusulas de 'arestas' (edge(2,1),etc.) ou poderíamos tentar uma regra como:

(*) edge(X,Y) :- edge(Y,X).

No entanto, esta não é uma boa ideia. Para ver por que não é uma boa ideia, tente o seguinte objetivo.

?- edge(5,1).

Observe que a regra (*) será tentada repetidamente em um loop infinito, de modo que o objetivo não será encerrado. Tente! A melhor maneira de lidar com isso é usar uma regra como a seguinte.

connected(X,Y) :- edge(X,Y) ; edge(Y,X).

Observe o uso da disjunção ';' nesta regra. Esta regra pode ter sido escrita como duas regras:

connected(X,Y) :- edge(X,Y).
connected(X,Y) :- edge(Y,X).

Queremos desenvolver uma definição de Prolog que gere caminhos entre quaisquer dois nós do grafo. Mais especificamente, exigimos o seguinte (tipo de) comportamento para o predicado 'paths'.

?- path(1,5,P).
P = [1,2,5] ;
P = [1,2,3,5] ;
P = [1,2,3,4,5] ;
P = [1,4,5] ;
P = [1,4,3,5] ;
P = [1,4,3,2,5] ;
P = [1,3,5] ;
P = [1,3,4,5] ;
P = [1,3,2,5] ;
no

Os caminhos são representados pela lista de nós através dos quais se deve viajar para ir do nó 1 ao nó 5. Aqui está uma definição para os caminhos:

path(A,B,Path) :-
       travel(A,B,[A],Q), 
       reverse(Q,Path).

travel(A,B,P,[B|P]) :- 
       connected(A,B).
travel(A,B,Visited,Path) :-
       connected(A,C),           
       C \== B,
       \+member(C,Visited),
       travel(C,B,[C|Visited],Path).

Uma leitura declarativa para a primeira cláusula equivale a "Um caminho de A para B é obtido se A e B estiverem conectados". Uma leitura declarativa para a segunda cláusula equivale a "Um caminho de A para B é obtido desde que A esteja conectado a um nó C diferente de B que não está na parte anteriormente visitada do caminho, e se continua encontrando um caminho de C para B". Evitar nós repetidos garante que o programa não funcionará continuamente.

Exercício 2.15 Suponha que as arestas tenham comprimentos. Como se calcula os caminhos mais curtos entre pontos no Prolog? Dica: pode-se usar o conjunto de objetivos, discutido na seção 2.12 e seção 4.15 ...

shortest(A,B,Path,Length) :-
   setof([P,L],path(A,B,P,L),Set),
   Set = [_|_], % fail if no path 
   minimal(Set,[Path,Length]).

Experimente este exercício (com a dica) antes de olhar para esta solução simplificada.

Veja Também

• Código do Prolog para esta seção.
• 2.12 Conjunto de respostas
• 2.16 Buscas em Prolog
• 4.15 Encontrando todas as respostas no prolog
• Prolog Tutorial Sumário