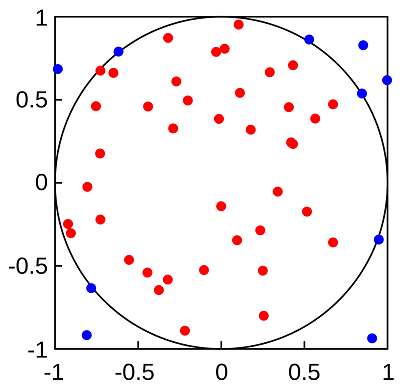
Estimating PI with Monte Carlo

Monte Carlo algorithms attempt to estimate through random sampling, as it can be time intensive to calculate the actual value. Monte Carlo makes use of random samples to generate a good estimate. There are many different Monte Carlo techniques, some of which are hybrids between Monte Carlo and other techniques. (Robert, 2005)

One simple example of Monte Carlo is its estimation of the value of PI

We will now place random points inside of the square and circle. The ratio of points inside to outside will tell us the value of PI. The area of the square is its length multiplied by its width. Because a square has the same width as length, the area of the square is essentially the width times itself, or width squared.

A área de um círculo é PI vezes seu raio ao quadrado. O diâmetro do círculo é igual à largura do quadrado. Vamos calcular a razão da área do círculo para o quadrado usando a equação abaixo.

[math] p = \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4}[/math]

A largura do quadrado é igual a duas vezes o raio do círculo. Portanto, podemos descrever o diâmetro do quadrado como duas vezes o raio ao quadrado. Tomaremos a proporção de pontos dentro do círculo para fora e multiplicaremos por 4. Isso nos dará uma aproximação de PI.

Exemplo em Python

Exemplo de sorteios

def estimate_pi(times = 10000, seed1=None, seed2=None):
    tries=0
    success=0

    # pick a point at random.
    if seed1 == None:
        t = time.perf_counter()
        seed1 = int(10**9*float(str(t-int(t))[0:]))
    x = pseudo_uniform(seed=seed1, size=times)

    if seed2 == None:
        t = time.perf_counter()
        seed2 = int(10**9*float(str(t-int(t))[0:]))
    y = pseudo_uniform(seed=seed2, size=times)

    for i in range(times):
        tries += 1

        # was the point inside of a circle?
        if x[i] * x[i] + y[i] * y[i] <= 1:
            success += 1
            
    pi = 4 * success / tries
    
    return pi

Exemplo:

import math

est_pi = estimate_pi(10000000, 123456789, 987654321)

print("Estimated PI: %f" % est_pi)
print("Real PI: %f" % math.pi)
print("Error: %f" % abs(est_pi - math.pi))

Estimated PI: 3.142123

Real PI: 3.141593

Error: 0.000531

Veja Também

• Gerador Aleatório Uniforme