Duas Definições de Fatorial
Duas definições de predicado que calculam a função fatorial estão no arquivo '2_2.pl', que o leitor pode visualizar clicando no link 'Código' ao finalo desta página. A primeira dessas definições é:
factorial(0,1).
factorial(N,F) :-
N>0,
N1 is N-1,
factorial(N1,F1),
F is N * F1.Este programa consiste em duas cláusulas. A primeira cláusula é uma cláusula unitária, sem corpo. A segunda é uma regra, porque tem um corpo. O corpo da segunda cláusula está no lado direito de ':-' que pode ser lido como um "se". O corpo consiste em literais separados por vírgulas ',' cada um dos quais pode ser lido como "e". O cabeçalho de uma cláusula é a cláusula inteira se a cláusula for uma cláusula unitária, caso contrário, o cabeçalho de uma cláusula é a parte que aparece à esquerda dos dois pontos em ':-'. Uma leitura declarativa da primeira cláusula (unidade) diz que "o fatorial de 0 é 1" e a segunda cláusula declara que "o fatorial de N é F se N>0 e N1 é N-1 e o fatorial de N1 é F1 e F é N*F1".
O objetivo do Prolog para calcular o fatorial do número 3 responde com um valor para 'W', a variável objetivo:
?- factorial(3,W).
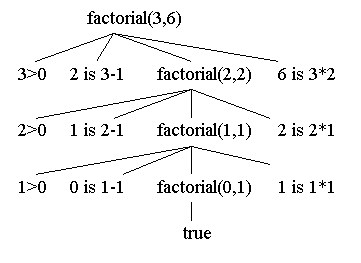
W=6Considere a seguinte árvore de cláusulas construída para o literal factorial(3,W). Conforme explicado na seção anterior, a árvore de cláusulas não contém nenhuma variável livre, mas, em vez disso, instâncias (valores) de variáveis. Cada ramificação em um nó é determinada por uma cláusula no programa original, usando instâncias relevantes das variáveis; o nó é determinado por alguma instância do cabeçalho de uma cláusula e os literais do corpo da cláusula determinam os filhos do nó na árvore de cláusulas.
Todas as folhas aritméticas são verdadeiras por avaliação (sob a interpretação pretendida), e o elo mais baixo na árvore corresponde à primeira cláusula do programa para fatorial. Essa primeira cláusula pode ser escrita
factorial(0,1) :- true.e, de fato, ?- true é uma meta do Prolog que sempre é bem-sucedida ('true' é nativo). Por uma questão de brevidade, não desenhamos folhas 'verdadeiras' sob os verdadeiros literais aritméticos.
A árvore de cláusulas do programa fornece um significado do programa para o objetivo na raiz da árvore. Ou seja, factorial(3,6) é uma consequência do programa Prolog, porque há uma árvore de cláusulas enraizada em factorial(3,6) cujas folhas são verdadeiras. O literal factorial(5,2), por outro lado, não é uma consequência do programa porque não há árvore de cláusulas enraizada em factorial(5,2) com todas as folhas verdadeiras. Assim, o significado do programa para o literal factorial(5,2) é que ele é falso. De fato,
?- factorial(3,6).
yes
?- factorial(5,2).
nocomo esperado. As árvores de cláusulas são chamadas de Árvores-E (AND-trees), uma vez que, para que a raiz seja uma consequência do programa, cada uma de suas subárvores também deve ser enraizada em literais que são, elas mesmas, consequências do programa. Teremos mais a dizer sobre as árvores de cláusulas posteriormente. Indicamos que as árvores de cláusulas fornecem um significado ou semântica para os programas. Veremos outra abordagem à semântica do programa no Capítulo 6. As árvores de cláusulas fornecem uma abordagem intuitiva, bem como correta, da semântica do programa.
Precisamos distinguir entre as árvores de cláusulas do programa e as chamadas árvores de derivação do Prolog. As árvores de cláusulas são "estáticas" e podem ser desenhadas para um programa e objetivo, independentemente do mecanismo processual de satisfação de objetivo específico. Grosso modo, as árvores de cláusulas correspondem à leitura declarativa do programa.
As árvores de derivação, por outro lado, levam em consideração o mecanismo de ligação de variáveis do Prolog e a ordem em que as subobjetivas são consideradas. As árvores de derivação são discutidas na Seção 3.1 (mas veja a animação abaixo).
Um traço de execução do Prolog também mostra como as variáveis são vinculadas para satisfazer os objetivos. O exemplo a seguir mostra como um rastreador Prolog típico é ligado e desligado.
?- trace.
% The debugger will first creep -- showing everything (trace).
yes
[trace]
?- factorial(3,X).
(1) 0 Call: factorial(3,_8140) ?
(1) 1 Head [2]: factorial(3,_8140) ?
(2) 1 Call (built-in): 3>0 ?
(2) 1 Done (built-in): 3>0 ?
(3) 1 Call (built-in): _8256 is 3-1 ?
(3) 1 Done (built-in): 2 is 3-1 ?
(4) 1 Call: factorial(2, _8270) ?
...
(1) 0 Exit: factorial(3,6) ?
X=6
[trace]
?- notrace.
% The debugger is switched off
yesA árvore animada abaixo dá uma outra visão da árvore de derivação para o objetivo do Prolog factorial(3,X). Para iniciar (ou reiniciar) a animação, basta clicar no botão "Step".
O título desta seção se refere a duas definições fatoriais. Aqui está o outro, com o mesmo nome de predicado, mas usando três variáveis.
factorial(0,F,F).
factorial(N,A,F) :-
N > 0,
A1 is N*A,
N1 is N -1,
factorial(N1,A1,F).Para esta versão, use o seguinte tipo de objetivo:
?- factorial(5,1,F).
F=120O segundo parâmetro na definição é um parâmetro de acumulação. Esta versão é apropriadamente recursiva na cauda. É muito importante que o aluno conclua os exercícios a seguir.
Exercício 2.2.1 Usando o primeiro programa fatorial, mostre explicitamente que não pode haver uma árvore de cláusulas enraizada em factorial(5,2) com todas as folhas verdadeiras.
Exercício 2.2.2 Desenhe uma árvore de cláusulas para o objetivo factorial(3,1,6) com todas as folhas verdadeiras, de uma forma semelhante à feita para o factorial(3,6) anteriormente. Como os dois programas diferem em relação ao modo como calculam o fatorial? Além disso, trace o objetivo factorial(3,1,6) usando Prolog.